|
|
 |
Каталог статей |
 |
Контрольная работа 28.1
Контрольная работа по теории вероятности (200р)
1. Профессор вызвал через старосту
на консультацию трёх студентов из шести отстающих. Староста забыл
фамилии вызванных студентов и послал наудачу трёх отстающих студентов.
Определить вероятность того, что староста послал именно тех студентов,
которых вызвал профессор.
2. Из 25 кинескопов, имеющихся в
телевизионном ателье, 5 штук произведены заводом № 1, 12 штук ‐ заводом №
2 и 8 штук – заводом № 3. Вероятность того, что кинескоп, изготовленный
заводом № 1 в течение гарантийного срока не выйдет из строя, равна
0,95. Для кинескопа завода № 2 такая вероятность равна 0,9, а для
кинескопа завода № 3 ‐ 0,8. Найти вероятность того, что наудачу взятый
кинескоп выдержит гарантийный срок.
3. Работают 10 станков. Вероятность включения станка равна 0,9. Найти вероятность того, что в данный момент включено 6 станков.
4.
Рабочий обслуживает три станка. Каждый станок в течение смены
останавливается по какой‐либо причине с вероятностью 0,2. Составить
закон распределения случайной величины X – числа остановок станков.
Найти его математическое ожидание, дисперсию, среднее квадратическое
отклонение.
5. Случайная величина X задана функцией распределения (интегральной функцией) F(x).
Найти:
а) дифференциальную функцию f(x) (плотность вероятности);
б) математическое ожидание и дисперсию;
в) вероятность попадания случайной величины в заданный интервал (a,b), то есть P(a<X<b).

6.
Случайная величина X распределена по нормальному закону с
математическим ожиданием a и средним квадратическим отклонением σ .
Записать плотность распределения f(x) и построить её график.
Найти вероятность попадания случайной величины в заданный интервал (α,β).
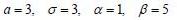
|
| Категория: Теория вероятностей и математическая статистика | Добавил: kontrolnresh (10.06.2012)
|
| Просмотров: 896
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
 |
Copyright MyCorp © 2025 |
 |
|